arviz.plot_loo_pit#

arviz.plot_loo_pit(idata=None, y=None, y_hat=None, log_weights=None, ecdf=False, ecdf_fill=True, n_unif=100, use_hdi=False, hdi_prob=None, figsize=None, textsize=None, labeller=None, color='C0', legend=True, ax=None, plot_kwargs=None, plot_unif_kwargs=None, hdi_kwargs=None, fill_kwargs=None, backend=None, backend_kwargs=None, show=None)[source]#

Plot Leave-One-Out (LOO) probability integral transformation (PIT) predictive checks.

Parameters:

idataInferenceData: arviz.InferenceData object.
yarray, DataArray or str: Observed data. If str, idata must be present and contain the observed data group
y_hatarray, DataArray or str: Posterior predictive samples for y. It must have the same shape as y plus an extra dimension at the end of size n_samples (chains and draws stacked). If str or None, idata must contain the posterior predictive group. If None, y_hat is taken equal to y, thus, y must be str too.
log_weightsarray or DataArray: Smoothed log_weights. It must have the same shape as y_hat
ecdfbool, optional: Plot the difference between the LOO-PIT Empirical Cumulative Distribution Function (ECDF) and the uniform CDF instead of LOO-PIT kde. In this case, instead of overlaying uniform distributions, the beta hdi_prob around the theoretical uniform CDF is shown. This approximation only holds for large S and ECDF values not very close to 0 nor 1. For more information, see Vehtari et al. (2021), Appendix G.
ecdf_fillbool, optional: Use matplotlib.axes.Axes.fill_between() to mark the area inside the credible interval. Otherwise, plot the border lines.
n_unifint, optional: Number of datasets to simulate and overlay from the uniform distribution.
use_hdibool, optional: Compute expected hdi values instead of overlaying the sampled uniform distributions.
hdi_probfloat, optional: Probability for the highest density interval. Works with use_hdi=True or ecdf=True.
figsize(float, float), optional: If None, size is (8 + numvars, 8 + numvars)
textsizeint, optional: Text size for labels. If None it will be autoscaled based on figsize.
labellerLabeller, optional: Class providing the method make_pp_label to generate the labels in the plot titles. Read the Label guide for more details and usage examples.
colorstr or array_like, optional: Color of the LOO-PIT estimated pdf plot. If plot_unif_kwargs has no “color” key, a slightly lighter color than this argument will be used for the uniform kde lines. This will ensure that LOO-PIT kde and uniform kde have different default colors.
legendbool, optional: Show the legend of the figure.
axaxes, optional: Matplotlib axes or bokeh figures.
plot_kwargsdict, optional: Additional keywords passed to matplotlib.axes.Axes.plot() for LOO-PIT line (kde or ECDF)
plot_unif_kwargsdict, optional: Additional keywords passed to matplotlib.axes.Axes.plot() for overlaid uniform distributions or for beta credible interval lines if ecdf=True
hdi_kwargsdict, optional: Additional keywords passed to matplotlib.axes.Axes.axhspan()
fill_kwargsdict, optional: Additional kwargs passed to matplotlib.axes.Axes.fill_between()
backendstr, optional: Select plotting backend {“matplotlib”,”bokeh”}. Default “matplotlib”.
backend_kwargsbool, optional: These are kwargs specific to the backend being used, passed to matplotlib.pyplot.subplots() or bokeh.plotting.figure(). For additional documentation check the plotting method of the backend.
showbool, optional: Call backend show function.

Returns:

axesmatplotlib Axes or bokeh_figures

See also

plot_bpv: Plot Bayesian p-value for observed data and Posterior/Prior predictive.
loo_pit: Compute leave one out (PSIS-LOO) probability integral transform (PIT) values.

References

Gabry et al. (2017) see https://arxiv.org/abs/1709.01449
https://mc-stan.org/bayesplot/reference/PPC-loo.html
Gelman et al. BDA (2014) Section 6.3

Examples

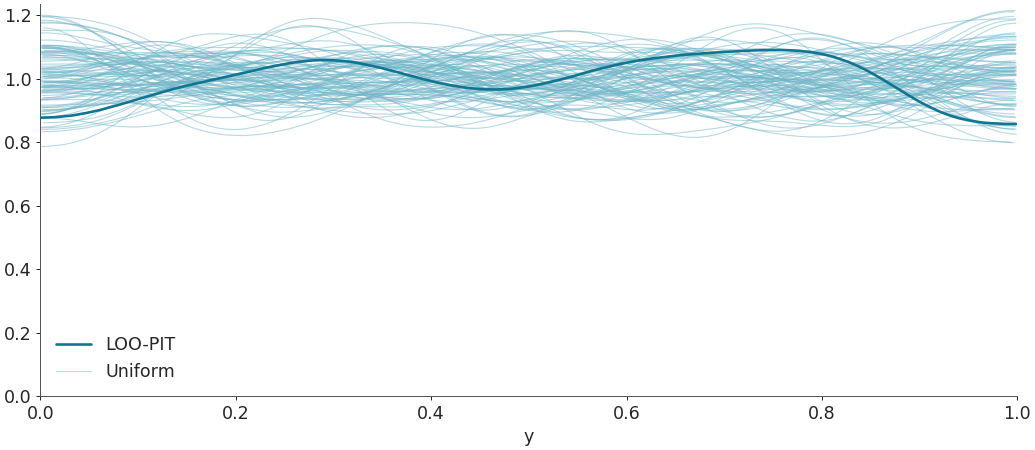
Plot LOO-PIT predictive checks overlaying the KDE of the LOO-PIT values to several realizations of uniform variable sampling with the same number of observations.

>>> import arviz as az
>>> idata = az.load_arviz_data("radon")
>>> az.plot_loo_pit(idata=idata, y="y")

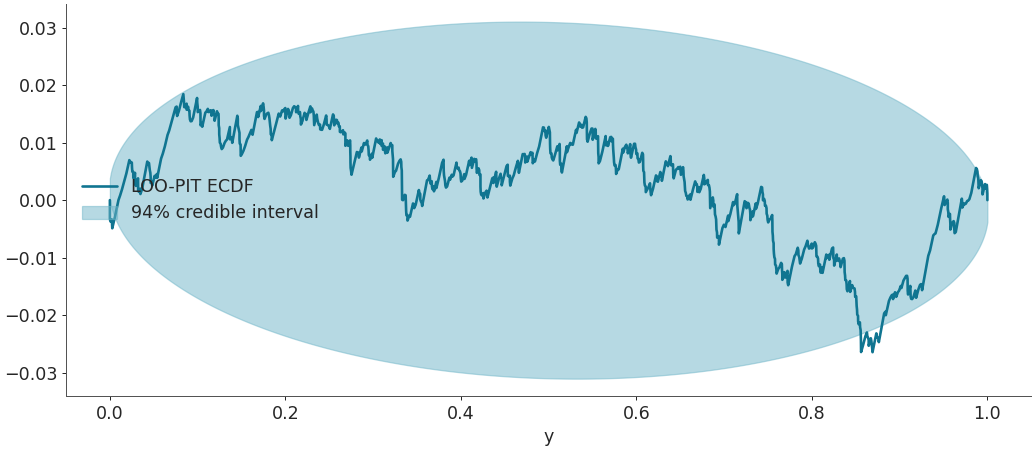
Fill the area containing the 94% highest density interval of the difference between uniform variables empirical CDF and the real uniform CDF. A LOO-PIT ECDF clearly outside of these theoretical boundaries indicates that the observations and the posterior predictive samples do not follow the same distribution.

>>> az.plot_loo_pit(idata=idata, y="y", ecdf=True)